

Acceleration is also a vector quantity, so it includes both magnitude and direction. This allows you to measure how fast velocity changes in meters per second squared (m/s2). Occasionally Sports announcers say that a person is accelerating if they are moving fast. Acceleration (a) is the change in velocity (v) over the change in time (t), represented by the equation a v/t. An object is still accelerating if it is changing its velocity time and again. Car Physics Acceleration examples: braking with constant force and decelerating with air resistance. Join Physics Forums Today The friendliest, high quality science and math community on the planet Register. A real world issue here is the total amount of mass involved, since the the total mass includes the mass of the spring itself. Using a spreadsheet for repetitive data handling.Īcceleration examples: braking with constant force and decelerating with air resistance. The definition of acceleration can be stated as: Acceleration can be defined as a vector quantity that defines the rate at which an object changes its velocity. The acceleration at the stop is the ratio of force / mass, and the force at the stop is always the same.
Acceleration physics software#
Using frame grabbing software and spreadsheet software to determine velocity and accleration of an object. Motion in one dimension under constant velocity or constant acceleration: deriving the equations from the definitions of velocity and acceleration.
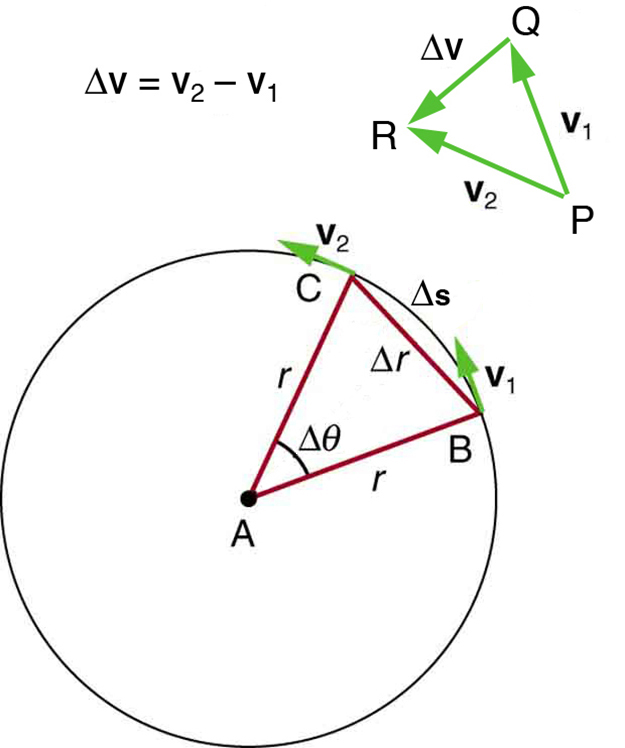
Vectors, vector components, unit vectors, two and three dimensions, vector addition and subtraction, relative motion and moving coordinates, the scalar product of vectors (the dot product), the vector product (the cross product) Links to related material and teachers' resourcesĪ simple, physics-based guide to quantities that vary: differentiation and integration, numerical and analytical, the log function, polynomials, trigonometric functions, the chain rule, techniques for integration, partial derivatives, introduction to logsĭrawing graphs, handling units and errors, significant figures, the method of dimensions, dealing with non-SI units


 0 kommentar(er)
0 kommentar(er)
